math references

Home

Screenshots courtesy of Math Academy

---

1. Calculating the inverse of a 3x3 matrix using the Cofactor Method

---

2. Calculating Individual Entries of the Matrix of Cofactors

---

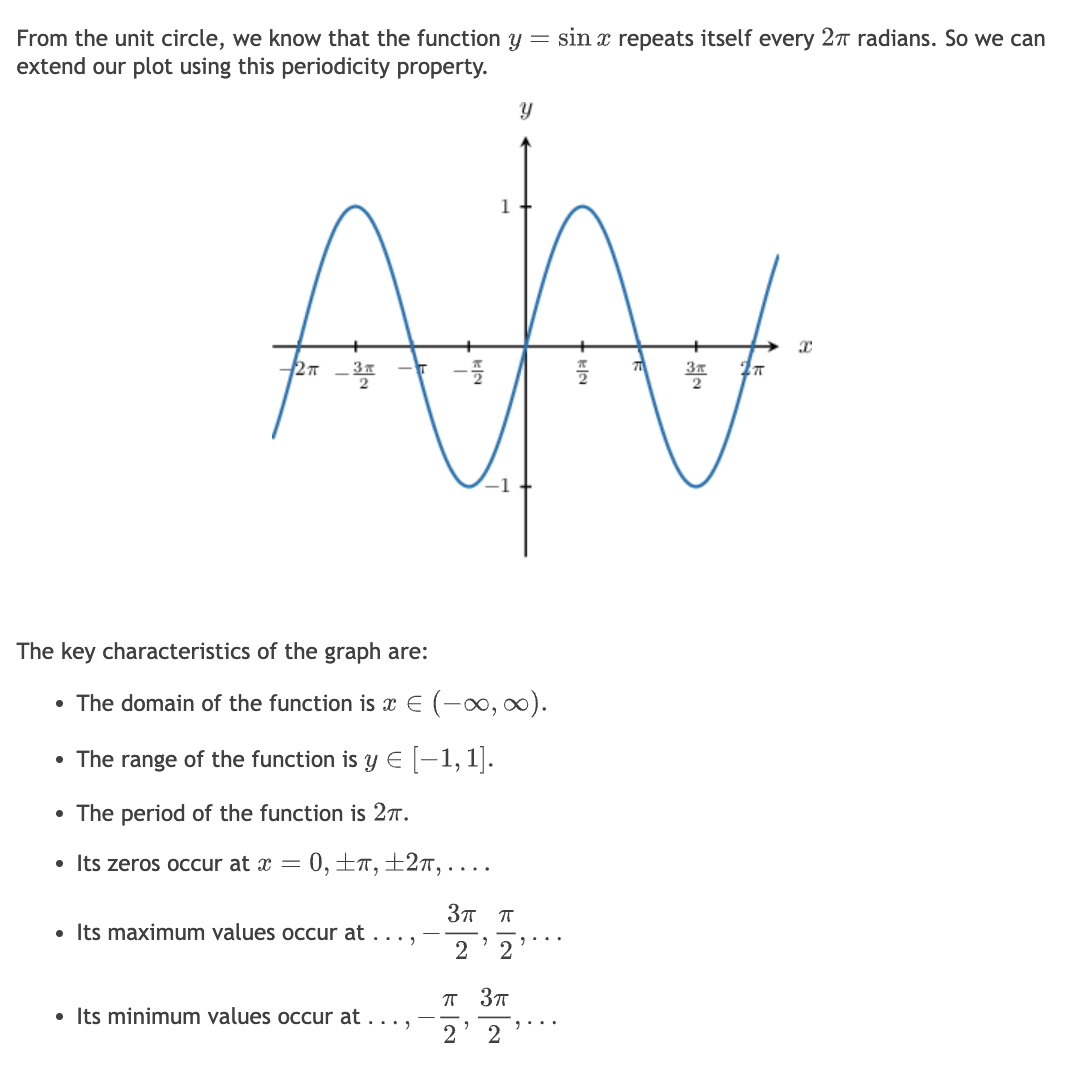
3. Sine Graph and Properties

---

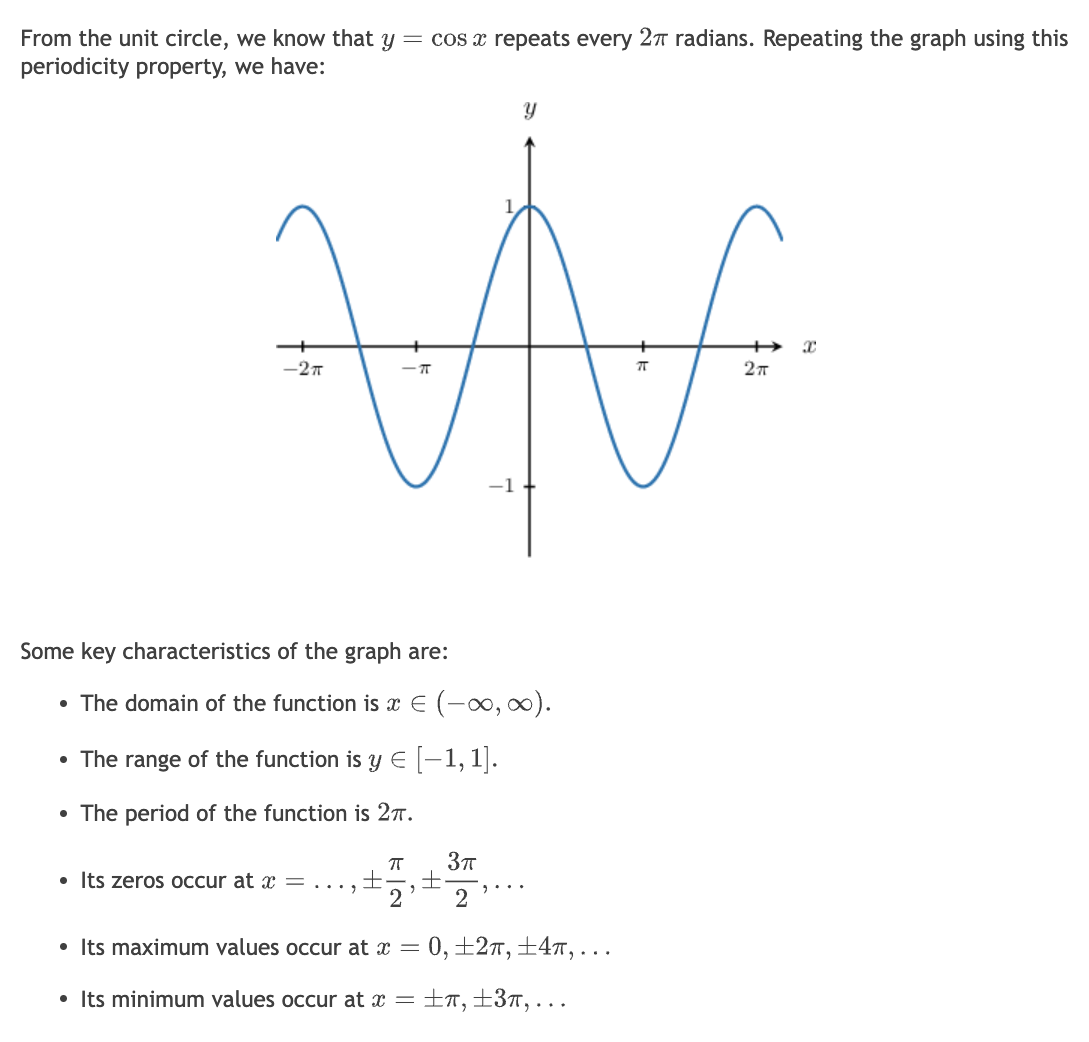
4. Cosine Graph and Properties

---

5. Invertible Matrix Theorem in Terms of 2x2 System of Equations

---

6. Trigonometric Derivatives

---

7. When should we use the absolute value when we take some sort of roots (sqrt, cube root, etc.)?

---

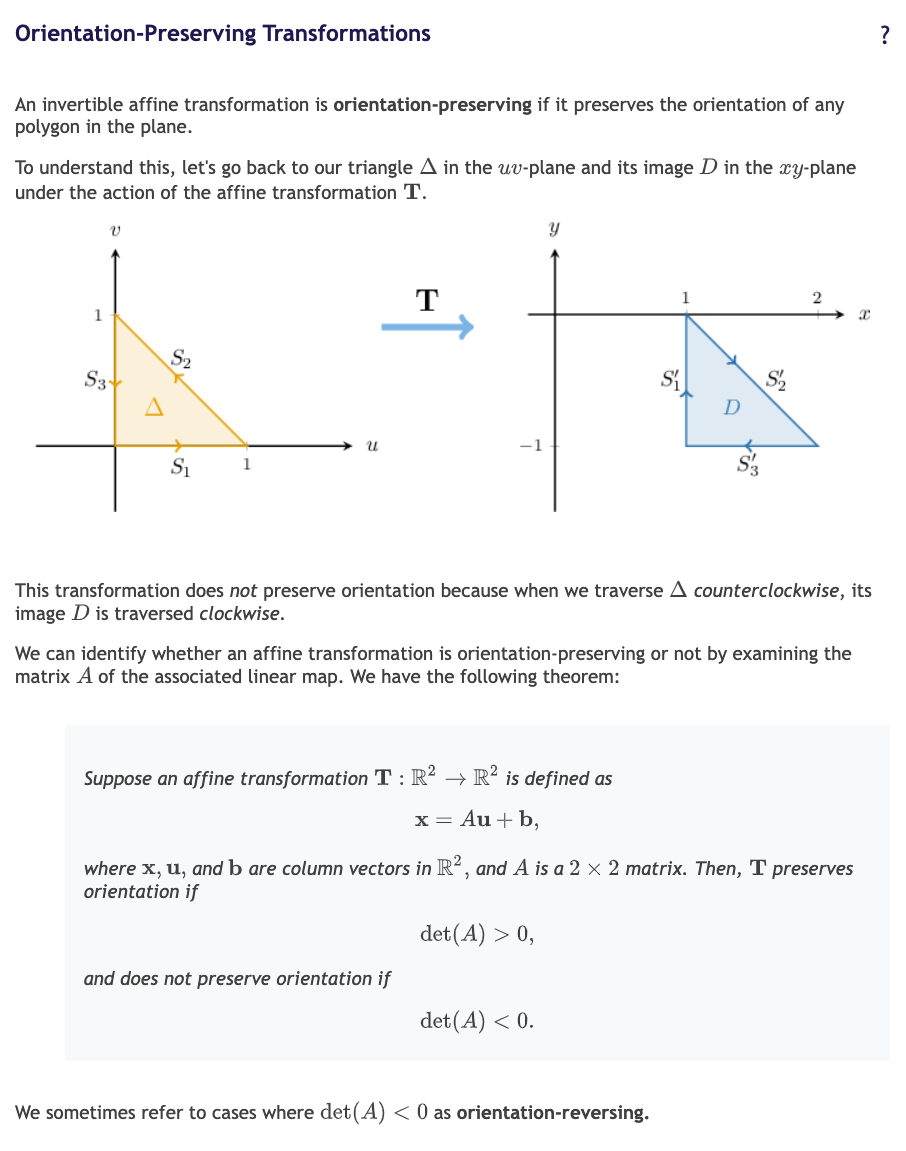
8. Orientation-Preserving Transformations

---

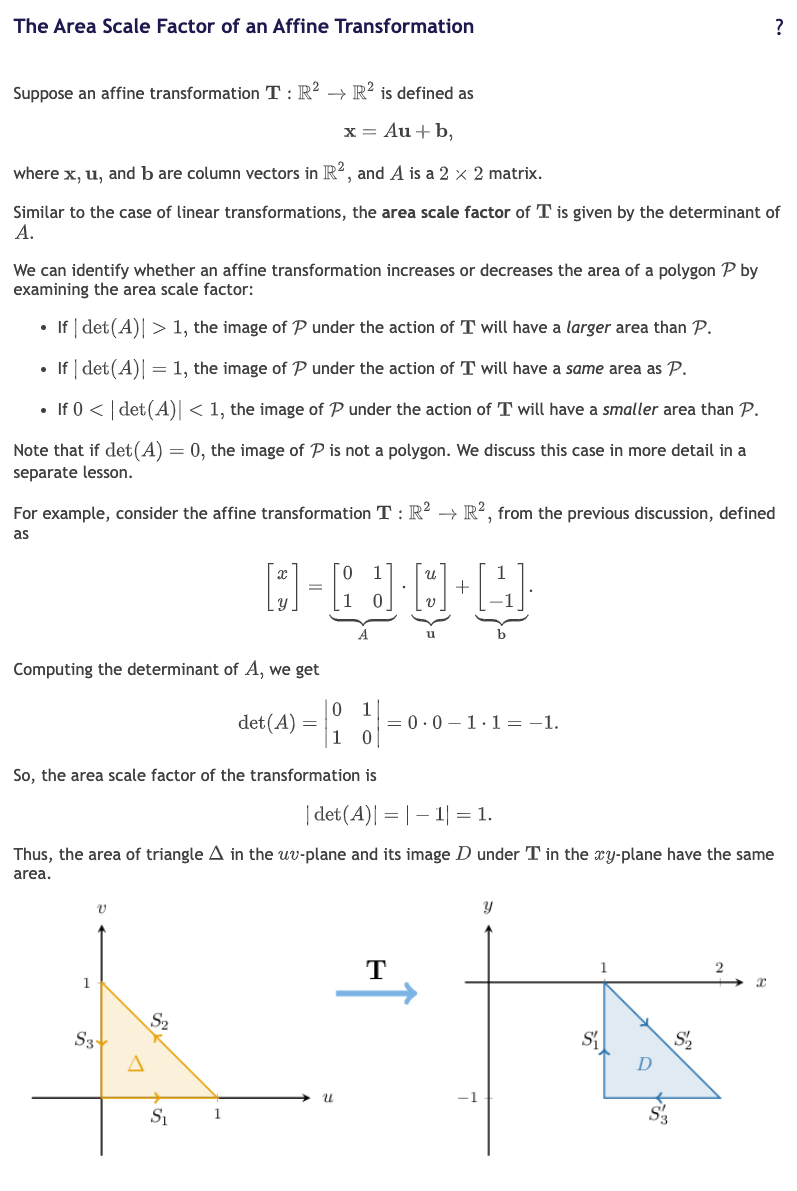
9. Area Scale Factor of an Affine Transformation

---

10. Different Types of Parabola Equations and their Significances

There are mainly 2 kinds of parabolic equations.

1. Standard Form (Vertex Form)

These equations describe parabolas based on their orientation along either the $x$-axis or the $y$-axis. They are often written as:

For a left- or right-opening parabola (horizontal orientation): $(y-k{)}^2=4p(x-h)$ For an upward or downward-opening parabola (vertical orientation):$(x-h{)}^2=4p(y-k)$ In these equations:

• $(h,k)$ is the vertex of the parabola.
• $p$ represents the distance from the vertex to the focus. If $p>0$, it opens to the right/up, and if $p<0$, it opens to the left/down.

Purpose of Standard Form:

• Useful for quickly identifying:
  • The direction the parabola opens (determined by whether $x$ or $y$ is squared).
  • The vertex $(h,k)$.
  • The distance from the vertex to the focus and the directrix.

2. General Form (Expanded Vertex Form)

This form is convenient for graphing transformations and is often written as:

For a vertically oriented parabola: $y=a(x-h{)}^2+k$ For a horizontally oriented parabola: $x=a(y-k{)}^2+h$ In these equations:

• $a$ controls the width and direction of the parabola.
• If $a>0$, the parabola opens upward (for vertical) or to the right (for horizontal).
• If $a<0$, it opens downward (for vertical) or to the left (for horizontal).
• $(h,k)$ is the vertex of the parabola.

Purpose of General Form:

• Useful for graphing because:
  • $a$ directly controls the stretch or compression of the parabola. A larger $|a|$ makes the parabola narrower, while a smaller $|a|$ makes it wider.
  • It’s easy to see transformations like vertical/horizontal shifts and reflections from this form.

So, in summary:

• Standard Form: Best for understanding focal properties, such as focus and directrix.
• General Form: Best for graph transformations like translations, stretches, and reflections.

---

Home