Autograd Logic

Note: This blog is not the final product; it is still a work in progress.

Gradient Lifetime

The aspect of zeroing out the gradients is very crucial. Where exactly does that occur? I need to understand and explain it.

My current understanding: The zeroing out part occurs right BEFORE each backward pass. The zeroed out gradient for any parameter then gets a total accumulation of its gradients across the network (say it is ). We will then use this gradient to update the parameter with the help of a small learning rate like this:

So, for instance, if we have a parameter , we first zero its gradient (zero_grad()), and then accumulate its gradients across the network (say it is ). We will then use this gradient to update the parameter with the help of a small learning rate like this:

python
COPIED
W1.data -= W1.grad * 0.01

As soon as we update the parameter's data here, we zero the so that we can do these exact same steps again in the next loop when we once again do .backward() (in which case, the parameter will have the newly updated data from the previous optimization, and so on). This continues until we have minimized the loss (without overfitting our data, of course).

Here, the 0.01 number is called the learning rate, and this determines how big of a "jump" we want the parameter gradient to make alongside a gradient descent "curve" (eventually ensuring it reaches as close to the global minimum as possible) without jumping too far and exceeding the global minimum.

Accumulation Mechanism

How is the scenario handled when the same parameter (say ) is used in 2 different layers? How are the gradients handled?

This means the gradients are just added! Of course, the way gradients are calculated can differ based on the kind of operation that is happening (maybe addition, multiplication, matmul, sigmoid, etc.), but assuming the gradients are getting calculated for the parameter in given 2 layers, they will be accumulated. Pretty straightforward.

Topological Order Nuance

My current understanding:

Let's say I have a computation like the following:

python
COPIED
x = Tensor([2.0], requires_grad=True)
y = 2 * x + 5.0
L = y + x
L.backward()

In this case, the computation graph, from left to right, follows a rough order from -> -> .

Since in here is the output, the .backward() being done to means we are calculating gradients in each node (maybe we're most likely doing it only for leaf nodes and not the intermediary tensors, so let me assume, for this instance, that the gradient accumulation occurs for leaf nodes only, i.e., the parameters), i.e., the derivative of with respect to each node, and accumulating gradients for each parameter that occurs more than once across the layers / forward pass.

The topological sort gets applied for the .backward() since in the network's normal shape, the flow is a forward flow, i.e., a rough order from -> -> . But the gradient accumulation starts from the output ( here), and in order to follow the right-to-left order (compared to the normal left-to-right order during the forward pass), we do topological sorting of the operations in autograd (flow of the operations from right to left, basically).

To be more specific, the topological sort for my example will be:

The sort ensures we always apply the chain rule in reverse order of operations creation. This is why my example's gradient for would be (from both and paths).

Non-Parameter Gradients

Should be extremely clear about the leaf nodes and intermediate tensors and whether the neural network is designed to accumulate all their gradients or only the leaf nodes' gradients (it's mostly only the leaf nodes).

1. What are leaf nodes anyway?
2. What are intermediate tensors?
3. Why is the requires_grad crucial here?

My understanding:

Leaf nodes are the "starting" nodes in a neural network beyond which there are no operations. So, in a way, leaf nodes are basically the parameters.

Intermediate tensors are the tensors that are generated through different operations within the netowork and are not our leaf parameters. For instance, for the following flow:

python
COPIED
x = Tensor([2.0], requires_grad=True)
y = 2 * x + 5.0
L = y + x
L.backward()

I thought the leaf nodes were and . That was incorrect. The leaf node is only , not .

Here, I am counting as a parameter as well, but our issue here is that it is not a leaf node but rather an intermediary. But since we need its gradient as well, we need to do retain_grad=True so that its gradient also gets tracked by the engine. The requires_grad=True is not necessary for intermediaries.

The requires_grad allows me to tell the neural network to track the gradients; however, in the flow above, I should do requires_grad=True for only (since this is my leaf node tensor) and retain_grad=True for (since this is my intermediary tensor).

Computational Graph Analysis

How is the computation graph build and freed? What does it even mean when I say "build a computation graph" and "free the computation graph"?

My understanding:

Computation graph here refers to a Directed Acyclic Graph (DAG) where the nodes are operations and the edges are tensors.

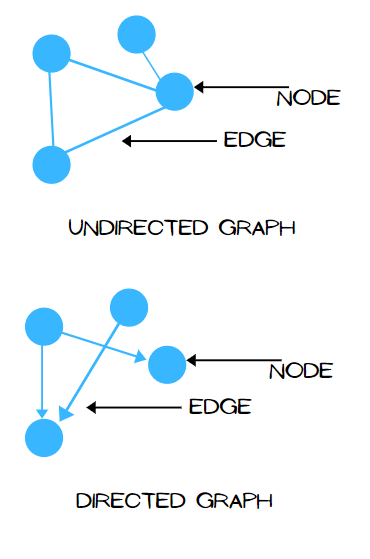
A simple illustration of a Directed Acyclic Graph (DAG). Source.

Building the graph happens during the forward pass by recording operations. Freeing the graph (lines 178-181 in my chibigrad implementation of PyTorch's tensor.py) involves clearing references to allow garbage collection, which was not mentioned. This is important for memory management, especially in large models.

What does "freeing the graph" or "graph destruction" mean?

PyTorch does this automatically unless I do retain_graph=True there.

Graph destruction is basically:

• Clearing the _backward_fn (the gradient calculation logic)
• Removing the operation reference (_op)
• Clearing input references (_inputs)

after a backward pass.

This is equivalent to PyTorch's graph destruction unless retain_graph=True. The graph exists to calculate gradients - once used, we free its memory unless explicitly retained.

Also, the question regarding retaining the grad: do we need to do retain_grad=True explicitly only for intermediates or is it also required for leaf nodes? Additionally, I do understand that we need to do requires_grad=True if we want any parameter's grad to be tracked, but does this mean that we need to do requires_grad=True and retain_grad=True for both the leaf node tensors as well as all the intermediate tensors? Or how does it work?

My understanding about retaining gradients:

Leaf nodes (like parameters) can just have requires_grad=True and their gradients are retained by default. For intermediates, like activation outputs, gradients aren't kept unless retain_grad() is called in addition to requires_grad=True. The retain_grad method sets _retain_grad to True, which prevents the warning when accessing .grad on non-leaf tensors. So in PyTorch, only leaf nodes retain gradients by default; intermediates need explicit retain_grad().

So, in summary:

• Leaf Nodes (parameters): Automatically retain gradients if requires_grad=True. No need for retain_grad()
• Intermediates: Need explicit retain_grad() to keep gradients
• requires_grad=True enables gradient computation tracking
• retain_grad=True enables gradient storage for non-leaf tensors

Example:

python
COPIED
# Leaf node (parameter) - gradient retained automatically
>>> w = torch.tensor([1.0], requires_grad=True)
>>> w
tensor([1.], requires_grad=True)

# Intermediate tensor - gradient not retained by default
>>> x = w * 2.0
>>> x
tensor([2.], grad_fn=<MulBackward0>)

>>> x.retain_grad() # Required to access x.grad later
>>> x
tensor([2.], grad_fn=<MulBackward0>)

>>> y = x + 1
>>> y
tensor([3.], grad_fn=<AddBackward0>)

>>> y.backward()

>>> print(w.grad)  # Works without retain_grad (leaf node)
tensor([2.])

>>> print(x.grad)  # Only works if retain_grad() was called
tensor([1.])

Now, let me try this exact same example but without using the retain_grad():

python
COPIED
>>> a = torch.tensor([1.0], requires_grad=True)
>>> b = a * 2.0
# Note that I did not do b.retain_grad() here

>>> c = b + 1
>>> c.backward()

>>> print(a.grad)
tensor([2.])

>>> print(b.grad)
<stdin>:1: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at /Users/runner/work/pytorch/pytorch/pytorch/build/aten/src/ATen/core/TensorBody.h:494.)
None # <- grad is none, and I also receive a big warning!